Elliptic Curve Cryptography: The Silent Guardian of Bitcoin!

Central to Bitcoin's security architecture is Elliptic Curve Cryptography (ECC), which has become the cornerstone of its encryption. But what is it exactly?
Let's take a look at how elliptic curves underpin the security of Bitcoin transactions, the principles behind them, and how this relates to Bitcoin L2s such as Bitfinity.
What is Elliptic Curve Cryptography?
To understand the mathematics behind the security of Bitcoin's cryptography, we need to understand Elliptic Curve Cryptography, which is a method of public-key cryptography based on the algebraic structure of elliptic curves over finite fields.
It is known for its ability to provide the same level of security as other cryptography methods but with smaller key sizes, leading to faster computations and lower power consumption.
It is used in various applications where high security and efficiency are crucial.
Think of 🤔:
- Many of the most popular secure messaging applications leverage ECC to facilitate end-to-end encryption, ensuring that only the intended participants in a conversation can access the messages. For instance, WhatsApp and Signal both use the open-source Signal Protocol, which employs Curve25519 for its Elliptic Curve Diffie-Hellman (ECDH) key agreement process.
- SSL/TLS protocols for secure internet communications are also one example of using this. In essence, this means that when you have a secure connection using the Transport Layer Security (TLS) protocol, ECC plays an instrumental role.
During the initial TLS "handshake" between your browser and a server, it performs two critical functions. It facilitates the key exchange (ECDHE) by generating a temporary key for each session, which provides "forward secrecy" to ensure past communications remain secure even if a server's main key is compromised.

- And Bitcoin...
As we know, ECC uses a pair of keys for encryption and decryption: a public key and a private key. The relationship between these keys involves elliptic curves, which we are going to explore below.
The Mathematics Behind ECC - How Does it Work?
The 'tech' behind ECC involves choosing a point on the curve and multiplying it by a predetermined number to get another point on the curve. This operation is easy to perform but difficult to reverse, which makes it optimal for encryption.
Another aspect of ECC is the use of a 'dot function', which involves adding points on the curve together. This addition is defined such that if you pick any two points on the curve and draw a line through them, it will intersect the curve at exactly one additional point.
An elliptic curve is a set of points that satisfies a specific mathematical equation, typically in the form y² = x³ + ax + b, along with a point at infinity. These curves can be graphed and look like smooth, symmetrical shapes about the x-axis.
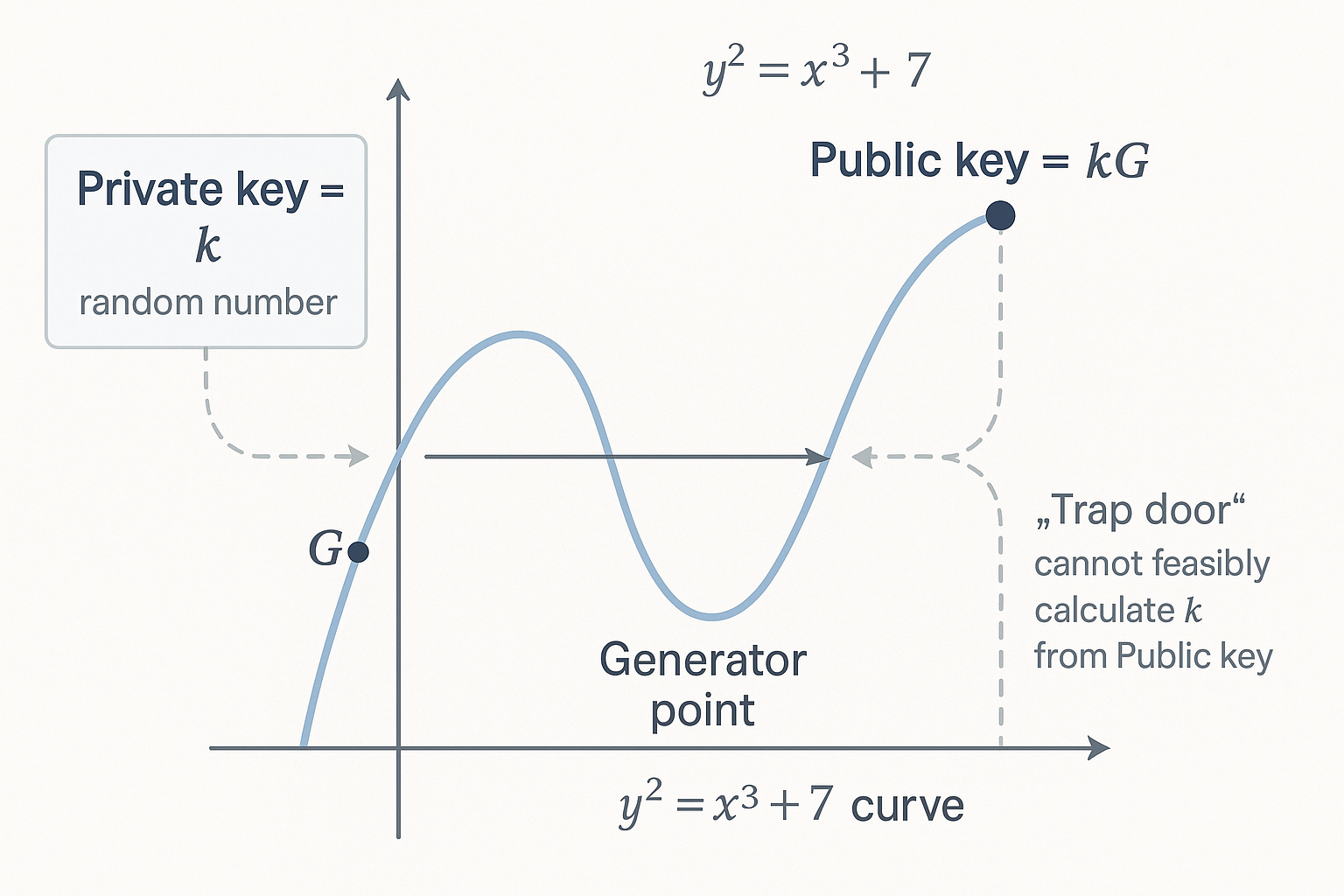
Public-Key Cryptography in Bitcoin
This encryption is then used for public-key cryptography, ensuring that it is virtually impossible to derive the private key if you know the public key. It also allows Bitcoin owners to prove they own their keys without revealing the private key.
Generation of Public and Private Keys
A private key is simply a randomly chosen number, and the corresponding public key is generated by multiplying this private key by a predefined point on the secp256k1 curve, known as the generator point "G".
This multiplication, due to the properties of the curve, does not allow for the private key to be feasibly calculated from the public key. This "trapdoor" function is what secures your private key against potential threats.
How Secure is ECC?
ECC offers a high level of security due to the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP), which is the basis for its security. Given a point on the curve and the result of multiplying that point by a number, it is computationally infeasible to determine that number.
This makes ECC particularly resistant against attacks, even if quantum computing is used, which underlines Bitcoin's security.

Securing Bitfinity's L2 Funds on the L1 Blockchain
Even though a Layer 2 solution like Bitfinity uses different cryptographic techniques for its operations, the funds held within its system are ultimately secured by a cryptographic commitment on the main Bitcoin blockchain.
For Bitfinity, this is achieved through an advanced mechanism called Chain-Key Cryptography, which uses a threshold Elliptic Curve Digital Signing Algorithm (tECDSA) scheme. Instead of locking Bitcoin into a simple multi-signature wallet, the funds are held in a Bitcoin address controlled collectively by a decentralized network of 40 nodes.
No single node has access to the full private key; instead, they hold key shares.

To move funds onto Bitfinity, a user creates a regular Bitcoin transaction, signing it with their private key to send BTC to the on-chain address controlled by Bitfinity's tECDSA system. This initial deposit is protected by the same reliable ECC that secures all Bitcoin transactions.
This process results in a standard Bitcoin transaction that is broadcast to the main network. The Bitcoin network can then validate this transaction using the public key corresponding to the tECDSA-controlled address, all without knowing the complex decentralised process that created the signature.
Bitfinity Inheriting Battle-Tested Security
By anchoring its bridge to the base layer, Bitfinity automatically benefits from the battle-tested security of the Bitcoin network.
While it introduces advanced off-chain concepts like an EVM-compatible environment and Chain-Key Cryptography, the transactions that lock and unlock BTC on the Bitcoin blockchain are standard, ECC-secured transactions.

The elliptic curve cryptography that has secured Bitcoin without a single breach of its base layer provides the foundational trust upon which Bitfinity must build. This allows Bitfinity's developers to focus on delivering scalability and a new experimentation ground for the Bitcoin layer.
Conclusion
Elliptic Curve Cryptography is the backbone of Bitcoin's security encryption (and also for other applications we take for granted), which means, in short, keys cannot be compromised because of...maths.
As Bitcoin continues to evolve with the development of Layer 2 solutions like Bitfinity, understanding the role of ECC becomes increasingly crucial.

Connect with Bitfinity Network
Bitfinity Wallet | Bitfinity Network | Twitter | Telegram | Discord | Github

*Important Disclaimer: The information provided on this website is for general informational purposes only and should not be considered financial or investment advice. While we strive for accuracy, Bitfinity makes no representations or warranties regarding the completeness, accuracy, or reliability of the content and is not responsible for any errors or omissions, or for any outcomes resulting from the use of this information. The content may include opinions and forward-looking statements that involve risks and uncertainties, and any reliance on this information is at your own risk.
External links are provided for convenience, and we recommend verifying information before taking any action. Bitfinity is not liable for any direct or indirect losses or damages arising from the use of this information.










Comments ()